Stirling's approximation

In mathematics, Stirling's approximation (or Stirling's formula) is an approximation for large factorials. It is named after James Stirling.
The formula as typically used in applications is
The next term in the O(n) is 1⁄2ln(2πn); a more precise variant of the formula is therefore
often written
Contents |
Derivation
The formula, together with precise estimates of its error, can be derived as follows. Instead of approximating n!, one considers its natural logarithm:
The right-hand side of this equation is (almost) the approximation by the trapezoid rule of the integral 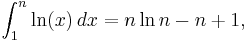 and the error in this approximation is given by the Euler–Maclaurin formula:
and the error in this approximation is given by the Euler–Maclaurin formula:
where Bk is a Bernoulli number and Rm,n is the remainder term in the Euler–Maclaurin formula. Take limits to find that
Denote this limit by y. Because the remainder Rm,n in the Euler–Maclaurin formula satisfies
where we use Big-O notation, combining the equations above yields the approximation formula in its logarithmic form:
Taking the exponential of both sides, and choosing any positive integer m, we get a formula involving an unknown quantity ey. For m=1, the formula is
The quantity ey can be found by taking the limit on both sides as n tends to infinity and using Wallis' product, which shows that 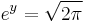 . Therefore, we get Stirling's formula:
. Therefore, we get Stirling's formula:
The formula may also be obtained by repeated integration by parts, and the leading term can be found through Laplace's method. Stirling's formula, without the factor 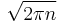 that is often irrelevant in applications, can be quickly obtained by approximating the sum
that is often irrelevant in applications, can be quickly obtained by approximating the sum
with an integral:
Speed of convergence and error estimates

More precisely,
with
Stirling's formula is in fact the first approximation to the following series (now called the Stirling series):
The first graph in this section shows the relative error vs. n, for 1 through all 5 terms listed above.

As 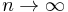 , the error in the truncated series is asymptotically equal to the first omitted term. This is an example of an asymptotic expansion. It is not a convergent series; for any particular value of n there are only so many terms of the series that improve accuracy, after which point accuracy actually gets worse. This is demonstrated in the next graph, which shows the relative error vs. the number of terms in the series.
, the error in the truncated series is asymptotically equal to the first omitted term. This is an example of an asymptotic expansion. It is not a convergent series; for any particular value of n there are only so many terms of the series that improve accuracy, after which point accuracy actually gets worse. This is demonstrated in the next graph, which shows the relative error vs. the number of terms in the series.
(More precisely, let 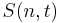 be the Stirling series to t terms evaluated at n. The graphs show
be the Stirling series to t terms evaluated at n. The graphs show 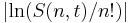 , which, when small, is essentially the relative error.)
, which, when small, is essentially the relative error.)
The asymptotic expansion of the logarithm is also called Stirling's series:
In this case, it is known that the error in truncating the series is always of the same sign and at most the same magnitude as the first omitted term.
Stirling's formula for the Gamma function
For all positive integers,
However, the Gamma function, unlike the factorial, is more broadly defined for all complex numbers other than non-positive integers; nevertheless, Stirling's formula may still be applied. If 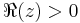 then
then
Repeated integration by parts gives
where Bn is the nth Bernoulli number (note that the infinite sum is non converging, so this formula is just an asymptotic expansion). The formula is valid for z large enough in absolute value when 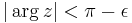 , where ε is positive, with an error term of
, where ε is positive, with an error term of 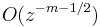 when the first m terms are used. The corresponding approximation may now be written:
when the first m terms are used. The corresponding approximation may now be written:
A convergent version of Stirling's formula
Thomas Bayes showed, in a letter to John Canton published by the Royal Society in 1763, that Stirling's formula did not give a convergent series.[1]
Obtaining a convergent version of Stirling's formula entails evaluating
One way to do this is by means of a convergent series of inverted rising exponentials. If 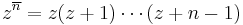 , then
, then
where
where 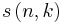 denotes the Stirling numbers of the first kind. From this we obtain a version of Stirling's series
denotes the Stirling numbers of the first kind. From this we obtain a version of Stirling's series
which converges when 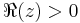 .
.
A version suitable for calculators
The approximation:
or equivalently,
can be obtained by rearranging Stirling's extended formula and observing a coincidence between the resultant power series and the Taylor series expansion of the hyperbolic sine function. This approximation is good to more than 8 decimal digits for z with a real part greater than 8. Robert H. Windschitl suggested it in 2002 for computing the Gamma function with fair accuracy on calculators with limited program or register memory (see link 'Toth').
Gergő Nemes[2] proposed in 2007 an approximation which gives the same number of exact digits as the Windschitl approximation but is much simpler:
or equivalently,
History
The formula was first discovered by Abraham de Moivre[1][2] in the form
De Moivre gave an expression for the constant in terms of its natural logarithm. Stirling's contribution consisted of showing that the constant is 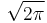 . The more precise versions are due to Jacques Binet.
. The more precise versions are due to Jacques Binet.
See also
- Lanczos approximation
- Spouge's approximation
Notes
- ↑ Le Cam, L. (1986), "The central limit theorem around 1935", Statistical Science 1 (1): 78–96 [p. 81], doi:10.1214/ss/1177013818, "The result, obtained using a formula originally proved by de Moivre but now called Sterling's formula, occurs in his `Doctrine of Chances' of 1733.".
- ↑ Pearson, Karl, "Historical note on the origin of the normal curve of errors", Biometrika 16: 402–404 [p. 403], "I consider the fact that Stirling showed that De Moivre's arithmetical constant was
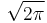 does not entitle him to claim the theorem."
does not entitle him to claim the theorem."
References
- Abramowitz, M. & Stegun, I. (2002), Handbook of Mathematical Functions, http://www.math.hkbu.edu.hk/support/aands/toc.htm
- Nemes, G. (2010), "New asymptotic expansion for the Gamma function", Archiv der Mathematik 95: 161-169, doi:10.1007/s00013-010-0146-9
- Paris, R. B. & Kaminsky, D. (2001), Asymptotics and the Mellin-Barnes Integrals, New York: Cambridge University Press, ISBN 0521790018
- Whittaker, E. T. & Watson, G. N. (1996), A Course in Modern Analysis (4th ed.), New York: Cambridge University Press, ISBN 0521588073
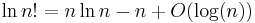
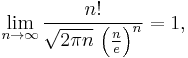
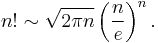
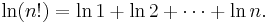
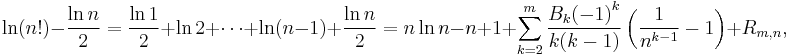
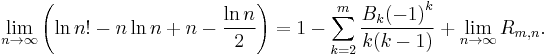
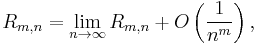
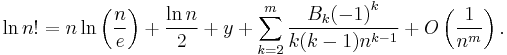
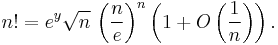
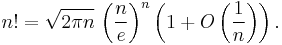
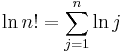
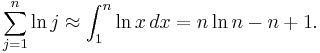
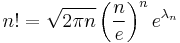
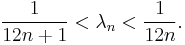
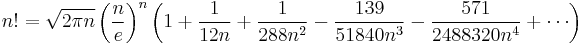
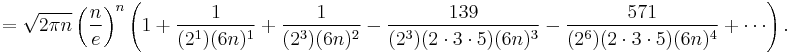
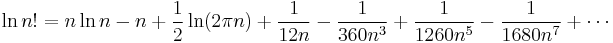
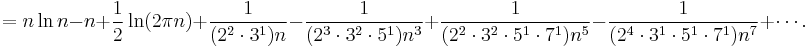
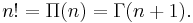
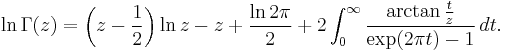
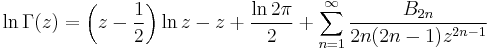
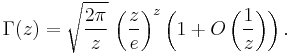
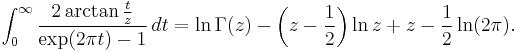
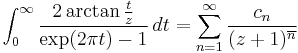
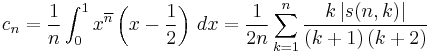
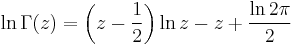
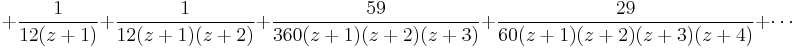
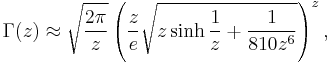
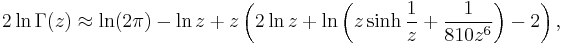
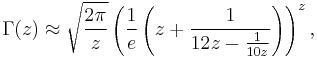
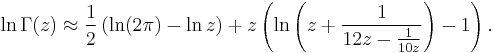
![n!\sim [{\rm constant}]\cdot n^{n+1/2} e^{-n}.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/a8a9589348e45ea88651a46690bfcde1.png)